|
|
Principal Manifolds 2006
|
|
Workshop
Principal manifolds
for data cartography and dimension reduction
August 24-26, 2006,
Michael Atiyah Building,
Lecture room 119
Leicester University,
Leicester, UK
You are welcome!
Registration and coffee 24.08.2006, at 9:30,
Opening 24.08.2006, at 10:00
International Organising Committee
Speakers that already confirmed their interest
Test datasets (microarray data)
The problems of Large Data Sets analysis and visualisation, model reduction and the struggle with complexity of data sets are important for many areas of human activity. There exist many scientific and engineering communities that attack these problems from their own sides, and now special efforts are needed to organize communication between these groups, to support exchange of ideas and technology transfer among them. Heuristic algorithms and seminal ideas come from all application fields and from mathematics also, and mathematics has a special responsibility to find a solid basis for heuristics, to transform ideas into exact knowledge, and to transfer the resulting ideal technology to all the participants of the struggle with complexity.
The workshop “Principal manifolds for data cartography and dimension reduction,” will be focused on modern theory and methodology of geometric data analysis and model reduction. Mathematicians, statisticians, engineers, software developers and advanced users form different areas of applications will attend this workshop.
During the Workshop the following activities will take place:
· Talks of internationally renowned experts;
· Demonstrations of the most up-to-date software;
· Demonstration of mapping and spatial analysis software and other GIS products;
· Active seminar in which different groups are given the same data to analyse and then they speak about their analysis of the data.
Free exploration of microarray data
Before coming to the workshop we propose to have a look at three datasets containing results of a high-throughput experimental technology application in molecular biology (microarray data). Principal component analysis and principal manifolds are highly demanded methods for analysis of this kind of data. It would be very interesting if you could apply your own methods to all or some of these datasets and present the results at the workshop such that we could compare them together.
The task could be free exploratory data analysis: any kind of message about the structure of the point distribution and relation of this structure to the proposed ab initio gene and sample classifications is interesting.
The multidisciplinary character of the workshop and the broad theme of discussion aims at eliminating some of the traditional language barriers that, unnecessarily sometimes, impede scientific cooperation and interaction of researchers across disciplines.
International Organising Committee
Prof Chris Brunsdon, Department of Geography, University of Leicester, UK.
Prof. Jean-Claude Golinval, Université de Liège, Belgium, Chairman of COST Action F3.
Prof. Alexander Gorban, Centre for Mathematical Modelling, University of Leicester, UK (chair).
Dr. Uwe Kruger, Intelligent Systems and Control Research Group, Queen's University of Belfast, UK
Prof Jeremy Levesley, Department of Mathematics, University of Leicester, UK
Prof Steven Damelin, IMA, University of Minnesota, USA
Prof. Donald Wunsch, Distinguished Professor of Computer Engineering at the University of Missouri – Rolla, President-Elect of the International Neural Networks Society, IEEE Fellow.
Dr. Andrey Zinovyev, Bioinformatics service, Institute Curie, Paris
Speakers that already confirmed their interest
Prof. Donald Wunsch, Distinguished Professor of Computer Engineering at the University of Missouri – Rolla, President-Elect of the International Neural Networks Society, IEEE Fellow;
Dr. A. Zinovyev, Bioinformatics service, Institute Curie, Paris, France;
Prof. Alexander Gorban, Centre for Mathematical Modelling, University of Leicester, UK;
Dr. Hujun Yin, School of Electrical and Electronic Engineering, The University of Manchester, UK
Dr. Stéphane Girard, INRIA Rhône-Alpes, France;
Prof Steven Damelin, IMA, University of Minnesota, USA
Prof Boris Mirkin Birkbeck College, University of London, UK
Dr. Jochen Einbeck, Department of Mathematics, National University of Ireland, Galway, Ireland;
Prof. Joachim Selbig, University of Potsdam and Max Planck Institute of Molecular Plant Physiology, Potsdam, Germany
Dr. Uwe Kruger, Intelligent Systems and Control Research Group, Queen's University of Belfast, UK
Dr. Andrew R. Webb, QinetiQ, Malvern, Worcestershire, UK
Prof. Colin Fyfe, Department of Computing and Information Systems, Paisley University, Paisley, Scotland, UK
Dr. David A. Elizondo, School of Computing, De Montfort University, Leicester, UK
Prof. Rodolphe Sepulchre, Department of Electrical Engineering and Computer Science, Université de Liège, Belgium.
Prof. Hans Troger, Institut für Mechanik Technische Universität Wien
Prof. Balazs Kegl, Dept. of Computer Science, University of Montreal, Canada
Dr. Liz Stuart, School of Computing, Communications and Electronics (SCCE), University of Plymouth
D. Wunsch will review the cluster analysis technique and its connection to dimension reduction approaches with application to homeland security.
A. Zinovyev will demonstrate a principal manifold based technology for Microarray visualization and analysis.
A. Gorban will present connections between nonlinear Galerkin approximations in physical applications and principal manifolds methods for data analysis, with applications for mesoscale modeling.
Hujun Yin will discuss adaptive data projection and visualisation methods, and connections between principal manifolds and SOM for various applications.
Steven. B. Damelin is expected to give talk on dimension reduction and its connections to Paley Weiner theorems in scattering and imaging.
Boris Mirkin will give a talk “Principal cluster analysis methods in different settings.”
S. Girard will present a talk about auto-associative models and generalized principal component analysis.
J. Einbeck will present a recent development of principal curves algorithms, a talk “Local principal curves.”
J. Selbig will present a talk "Integrated analysis of metabolite, gene expression, and other profile data: Missing value estimation, dimension reduction, clustering, and classification".
U. Kruger will present principal manifolds and nonlinear principal component based methods for multivariate statistical process control with example of application for diagnosis of faults on internal combustion engines.
Colin Fyfe will present a talk “A family of topology preserving mappings for data visualisation”.
D.A. Elizondo will give a talk “Geometrical approaches for Artificial Neural Networks”
Rodolphe Sepulchre will present optimization-based numerical algorithms on manifolds with applications to PCA and ICA.
Balazs Kegl will give a general overview of manifold learning, presenting the achievements of the last ten years and the challenges of future research.
A. Steindl and H. Troger, “Invariant manifolds in the dimension reduction for fluid conveying tubes”
Liz Stuart will present a talk “An Overview of Visualization Techniques for the Analysis of Large Datasets”
Ludger Evers (Department of Statistics, University of Oxford) will give a talk “A simple algorithm for piecewise linear approximation to principal manifolds and its application to regression modelling”
The workshop will deal with the subjects of principal manifolds, dimension reduction, data visualization and their applications. One of the goals is to investigate new and innovative concepts of defining principal curves/surfaces and to discuss new GIS-inspired technologies of data representation on these surfaces.
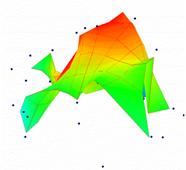
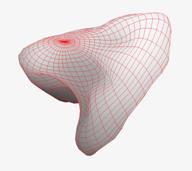
Principal manifolds were introduced by Hastie and Stueltze in 1984, 1989 as lines or surfaces passing through ``the middle'' of the data distribution [1]. This intuitive definition was supported by mathematical notion of self-consistency: every point of the principal manifold is a conditional mean of all points that are projected into this point. In the case of datasets only one or zero data points are projected in a typical point of the principal manifold, thus, one has to introduce smoothers that become an essential part of the principal manifold construction algorithms.
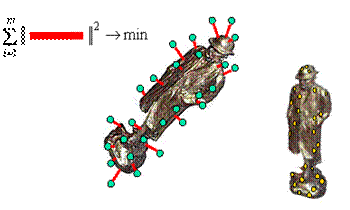
Since the pioneering work of Hastie, many modifications and alternative definitions of principal manifolds have appeared in the literature. Many alternative definitions were introduced (see, for example, [2]) in order to improve the situation and to allow the construction of principal curves (manifolds) for a distribution of points with several finite first moments. A promising approach is based on analogy of principal manifold and elastic membrane. The idea of using the elastic energy functional for principal manifold construction in the context of neural network methodology was proposed in mid 1990s (see [3] and bibliography there). Another computationally effective and robust algorithmic kernel for principal curve construction, called the polygonal algorithm, was proposed by Kegl et al [2]. A variant of this strategy for constructing principal graphs was also formulated in the context of the skeletonization of hand-written digits. An interesting approach we would also like to mention is the construction of principal manifolds in a piece-wise manner by fitting unconnected line segments [4].
Perhaps most scientific and industrial applications of principal manifold methodology were implemented using the SOM (self-organizing map) approach, coming from the theory of neural networks [5]. These applications are too numerous to be mentioned here. We only mention that SOMs, indeed, can provide principal manifold approximations (for example, see [6]) and are computationally effective. The disadvantage of this approach is that it is entirely based on heuristics; also it was shown that in the SOM strategy there does not exist any objective function that is minimized by the training process [7].
In applications of principal manifolds to 3D-surface modeling, one can find similar “physics-based” new methods in surface modeling in computer graphics (see, for example [8], [9]). A parametric model based on the generative topographic mapping, and the expectation-minimization algorithm to optimize the parameters was analyzed in [10].
One important application of principal manifolds is dimension reduction and data visualization. In this field they compete with multidimensional scaling methods and the recently introduced advanced algorithms of dimension reduction, such as locally linear embedding (LLE) [11] and ISOMAP [12] algorithms. The difference between the two approaches is that the later ones seek new point coordinates directly and do not use any intermediate geometrical objects. This has several advantages, in particular that a) there is a unique solution to the problem (the methods are not iterative in their nature, there is no problem of grid initialization) and b) there is no problem of choosing a good way to project points onto a non-linear manifold. Another advantage is that the methods are not limited by several first dimensions in dimension reduction (it is difficult in practice to manipulate non-linear manifolds of dimension more than three).
Using principal manifolds as a non-linear low-dimensional screen to project data gives other benefits. First, the manifold approximates data and can be used itself, without applying projection, to visualize different functions defined in data space (for example, density estimation). Also the manifold as an intermediate object for “fixing” the structure of a learning dataset, can be used in visualization of data points that were not used in the learning process, for example, for visualization of dataflow “on the fly”. Here we can find many links to modern GIS technologies.
LLE and ISOMAP methods are more suitable if the low-dimensional structure in multidimensional data space is complicated but is expected to exist, and if the data points are situated rather tightly on it. Principal manifolds are more applicable for the visualization of real-life noisy observations, appearing in economics, biology, medicine and other sciences, and for constructing data screens showing not only the data but different related functions defined in data space.
“The data mining community has tended to focus on the algorithmic aspects of pattern discovery, and has not developed a general underlying theoretical base. However, such a base is important for any technology: it helps to steer the direction in which the technology develops, as well as serving to provide a basis from which algorithms can be compared, and to indicate which problems are the important ones waiting to be solved.” [14] Principal manifold theory is an important element in this base.
During the workshop modern development of this direction will be present, as well as many recent applications, from engineering to bioinformatics.
1. T. Hastie, W. Stuetzle, Principal curves, Journal of the American Statistical Association 84 (406) (1989), 502-516.
2. B. Kegl, A. Krzyzak, T. Linder, K. Zeger, A polygonal line algorithm for constructing principal curves, Neural Information Processing Systems 1998, MIT Press, 1999, 501-507.
3. Gorban, A. Zinovyev, Elastic Principal Graphs and Manifolds and their Practical Applications, Computing 75 (2005), 359–379. (See also)
4. J.J. Verbeek, N. Vlassis, B. Krose, A k-segments algorithm for finding principal curves, Technical report, 2000. Online: http://citeseer.nj.nec.com/article/verbeek00ksegments.html.
5. T. Kohonen: Self-organized formation of topologically correct feature maps, Biological Cybernetics, 43 (1982), 59-69.
6. F. Mulier, V. Cherkassky: Self-organization as an iterative kernel smoothing process, Neural Computation 7 (1995), 1165-1177.
7. E. Erwin, K. Obermayer, K. Schulten, Self-organizing maps: ordering, convergence properties and energy functions, Biological Cybernetics 1992 (67), 47-55.
8. Chang K, Ghosh J, A unified model for probabilistic principal surfaces, IEEE Transactions on Pattern Analysis and Machine Intelligence 23 (1): 22-41.
9. Mandal C., Qin H., Vemuri B.C. A novel FEM-based dynamic framework for subdivision surfaces. 2000. Comp.-Aided Design 32. p.479-497.
10. Xie H., Qin H. A Physics-based Framework for Subdivision Surface Design with Automatic Rules Control. In Proceedings of the Tenth Pacific Conference on Computer Graphics and Applications (Pacific Graphics 2002), IEEE Press, p.304-315.
11. Roweis S. and Saul L. K. Nonlinear dimensionality reduction by locally linear embedding. 2000. Science 290. p. 2323-2326.
12. Tenenbaum J. B., De Silva V. and Langford J. C. A global geometric framework for nonlinear dimensionality reduction. 2000. Science 290. rp.2319-2323.
13. V. Pestov, On the geometry of similarity search: dimensionality curse and concentration of measure, Information Processing Letters 73 (2000), 47-51.
14. Hand, D. J. and R. J. Bolton (2004) Pattern Discovery and Detection: A Unified Statistical Methodology, Journal of Applied Statistics, 31(8), 885-924.
Contact:
|
Prof. Alexander Gorban Telephone - +44 (0) 116
223 14 33 |
Postal: Department of
Mathematics, Leicester LE1 7RH,
|