Alexander GORBAN
Professor, Chair in Applied
Mathematics,
Department of Mathematics,
University of Leicester, UK
E-mail: ag153@le.ac.uk
Full Professor in Modeling
& Simulation
Russian State Certificate of Professorship, 1993
Fellow of the Higher Education Academy (UK), 2016
Research interests:
Dynamics of systems of physical, chemical and biological kinetics; Data Mining;
Bioinformatics; Human adaptation to hard living conditions;
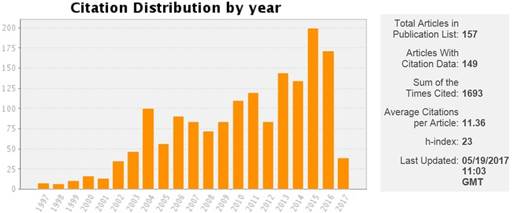
Citation information
- Web of Science citation index 1693, h-index 23
(19/05/2017),
WoS Researcher ID: D-7310-2011, http://www.researcherid.com/rid/D-7310-2011
Scopus citation score: citations 2108,
h-index 25 (19/05/2017),
Scopus Author ID: 7005285942 http://www.scopus.com/authid/detail.uri?authorId=7005285942#

- Google Scholar citation index 7172, h-index 41 (19/05/2017).
http://scholar.google.co.uk/citations?user=D8XkcCIAAAAJ&hl=en

Academic degrees
· 1980, PhD in Physics & Math (Differential Equations & Math.Phys), Kuibyshev, USSR. Thesis: "Slow Relaxations and Bifurcations of Omega-Limit Sets of Dynamical Systems";
· 1990, Doctor of Physics & Math (Biophysics), (Advanced doctoral degree, Dr. Sc., analogue of Dr Habilit.), Institute of Biophysics, Russian Academy of Sciences, Krasnoyarsk, USSR. Thesis: "Extremal Principles and a priori Estimations in Biological and Formal Kinetics".
· 1993, Full Professor in Modelling & Simulation: Russian State Certificate of Professorship.
Appointments
2004-present, University of Leicester:
· 2006-present, Director of the Centre for Mathematical Modelling;
· 2004-present, Chair in Applied Mathematics;
2003-2004, Swiss Federal Institute of technology (ETH), Zurich, Switzerland):
· Senior Researcher, 2003-2004;
1983-2005, Institute of Computational Modelling, Russian Academy of Sciences, Siberian Branch, Krasnoyarsk, Russia (last years was on leave):
· Deputy Director and Head of the Computer Sciences Department, 1995 – 2005;
· Head of the Nonequilibrium Systems Laboratory, 1989 – 2006;
· Senior researcher, 1983-1989;
· Junior researcher, 1978-1983;
1977-1978, Institute of Catalysis, USSR Academy of Sciences, Siberian Branch, Novosibirsk, Russia:
· Engineer, 1977-1978;
1978, Institute of Theoretical & Applied Mechanics, USSR Academy of Sciences, Siberian Branch, Novosibirsk, Russia:
· Engineer, 1978;
1977, Tomsk Polytechnic University, Laboratory of Kinetics, Tomsk, Russia:
· Junior researcher, 1977;
1976, Omsk State University, Laboratory of Kinetics, Omsk, Russia:
Junior researcher, 1976;
1973-1976, Omsk Railway Engineering Institute, Research Division, Omsk, Russia:
· Engineer, 1973-1976.
Part-time teaching
Krasnoyarsk State Technical University, Krasnoyarsk, Russia: (last years was on leave):
· Head of Neurocomputers Department, 1993-2006; Professor, 1993-2006;
Krasnoyask State Technological University, Krasnoyarsk, Russia:
· Professor, Department of Automatization and Robots, 1993-2003;
Krasnoyarsk State University, Krasnoyarsk, Russia:
· Professor, Psychological Faculty, 1998-2001;
· Associate professor, Higher Mathematics Chair, 1981-1989.
Visiting:
- Isaac Newton Institute for Mathematical Sciences (Cambridge, UK), 2010;
- Institut des Hautes Etudes Scientiques (IHES, Bures-sur-Yvette, France), 2000, 2001, 2002, 2003, 2009.
- Courant Mathematics Institute (New York, USA), 2000, 2007, 2008;
- Clay Mathematics Institute (Cambridge, USA), 2000 (Clay Scholar);
- ETH, Zurich, Switzerland: 1999, 2000, 2002.
Expert positions:
· Vice-Chairman of Scientific Council at Krasnoyarsk State Technical University (direction: Software and tools for mathematical modelling) (1999-2006);
· Head of Workgroup on Neurocomputing, Ministry of Science and Technology Russian Federation (1998-2000);
· Vice-Chairman of Expert Council Krasnoyarsk Regional Science Foundation (1993-1996);
· Chairman of the Analytic Games Committee, Krasnoyarsk (1989-1994);
· Member of Jury of USSR National competition in mathematics for students of technical universities (1986-1990).
Membership of Associations
· Member of SIAM;
· Member of LMS;
· Russian Society of Artificial Intelligence (Chair of Krasnoyarsk Regional Branch);
· Russian Neural Networks Society;
· Associated Member of ASME (American Society of Mechanical Engineers) (1997);
Grants and awards:
· Lead Academic in KTP010604 between Dataffirm Limited and the University of Leicester (Mining of Big Text Data), 2017-2019, £158K
· Lead academic in KTP 010522 between Visual Management Systems Ltd and University of Leicester (Visual Intelligence), 2016-2019 (approved in Aug 2016), £189K
· Lead academic in KTP 009890 between Apical Ltd and the University of Leicester (Visual Intelligence), 2015-2018 (approved in Dec 2014), £179K
· International Research Workshop: Hilbert’s Sixth Problem, LMS, 2016;
· International Research Workshop: Hilbert’s Sixth Problem, EPSRC, 2016;
· Lifetime Achievement Award in recognition of outstanding contributions to the research field of (bio)chemical kinetics, MaCKIE-2015, Mathematics in (bio)Chemical Kinetics and Engineering, Ghent, Belgium, 2015.
· Lattice Boltzmann methods for analysis of permeability in geophysics, Weatherford Contract Research, 07.2013 06.2015;
· Data Mining for Geological Information, NERC (Natural Environment Research Council), 07.2013 10.2013;
· Data Mining for Lymphoma Differential Diagnosis, European Regional Development Fund, 2012;
· Isaac Newton Institute for Mathematical Sciences Fellowship (Cambridge, UK), 2010
· Mathematical Modelling of Adaptation and Decision-Making in Neural Systems, The Royal Society, UK: International Joint UK-Japan Project;
· Modularity, Abstraction and Robustness of Network Models in Molecular Biology, Alliance : Franco-British Research Partnership Programme;
· EPSRC and LMS grants for the International Workshop “Model Reduction and Coarse-Graining Approaches for Multiscale Phenomena,” Leicester, UK August 24-26 2005;
· Prigogine Award and Medal (2003);
· Clay Scholar, (Clay Mathematics Institute, Cambridge, USA, 2000);
· Russian Federal Grant of the “Integration” program, 4 times (1998-2003);
· Grant of Russian Federal subprogram “New Information Processing Technology” (1999);
· Russian Federal Fellowship for outstanding scientists, twice (6 years);
· Grant of Russian Foundation of Basic Research (1996-1998);
· 1994-1996 American Mathematical Society Fellowship.
Scientific advisor of 29 PhD (candidate) theses, 5 DrSc, and 2 Habilitation Dr including:
· A. Zinovyev, Dealing with complexity of biological systems: from data to models, (Dr. Habilitation, Department of Biology of Ecole Normale Superieure, Paris, 2014)
· O. Radulescu, Mathematical models of complexity in molecular biology and mechanics of complex fluids, (Dr. Habilitation, Applied Mathematics, Université de Rennes 1, France, 2006)
· A.I. Legalov, Programming language tools for developing of transferrable and evolutionary extensible parallel programs (DrSc=“doctor nauk”, Computer Sciences, Krasnoyarsk State Technical University, Krasnoyarsk, 2005)
· M.G. Sadovskii, Statistical and informational properties of nucleotide sequences, (DrSc=“doctor nauk”, Biophysics, Institute of Biophysics Russian Academy of Sciences, Krasnoyarsk, 2004)
· E.M. Mirkes, The structure and functioning of ideal neurocomputer (DrSc=“doctor nauk”, Computer Science, Krasnoyarsk State Technical University, Krasnoyarsk, 2002);
· E.V. Smirnova, Mathematical modeling of adaptation, group stress and correlation adaptometry (DrSc=“doctor nauk”, Biophysics, Institute of Biophysics Russian Academy of Sciences, Krasnoyarsk, 2001);
· D.A. Rossiev, Neural networks based expert systems for medical diagnostics (DrSc=“doctor nauk”, Biophysics, Institute of Biophysics Russian Academy of Sciences, Krasnoyarsk,1997);
· Y. Shi, kNN Predictability Analysis of Stock and Share Closing Prices, (PhD, Applied Mathematics, University of Leicester, UK, 2016).
· A. Akinduko, Multiscale Principal Component Analysis (PhD, Applied Mathematics, University of Leicester, UK, 2015).
· D. Packwood, Non-Equilibrium Dynamics of Discrete Time Boltzmann Systems (PhD, Applied Mathematics, University of Leicester, UK, 2012).
· Jianxia Zhang, Nonequilibrium Entropic Filters for Lattice Boltzmann Methods and Shock Tube Case Studies (PhD, Applied Mathematics, University of Leicester, UK, 2012).
· M. Shahzad, Slow Invariant Manifold and its approximations in kinetics of catalytic reactions, (PhD, Applied Mathematics, University of Leicester, UK, 2011).
· H.A. Wahab, Quasichemical Models of Multicomponent Nonlinear Diffusion (PhD, Applied Mathematics, University of Leicester, UK, 2011).
· A.Yu. Zinovyev, Method of Elastic Maps for Data Visualization: Algorithms, Software and Applications in Bioinformatics (PhD=“kandidat nauk”, Computer Science, Krasnoyarsk State Technical University, Russia, 2001);
· V.G. Tzaregorodtzev, Algorithms, technology and software for knowledge extraction using trainable neural networks (PhD=“kandidat nauk”, Computer Science, Krasnoyarsk State Technical University, Russia, 2000);
· A.A. Pitenko, Neural networks for geoinformatics (PhD=“kandidat nauk”, Computer Science, Krasnoyarsk State Technical University, Russia, 2000);
· A.A. Rossiev, Neural network modeling of data with gaps (PhD=“kandidat nauk”, Computer Science, Krasnoyarsk State Technical University, Russia, 2000);
· M.Yu. Senashova, Accuracy estimation for neural networks (PhD=“kandidat nauk”, Computer Science, Krasnoyarsk State Technical University, Russia, 1999);
· M.A. Dorrer, Psychological intuition of neural networks (PhD=“kandidat nauk”, Computer Science, Krasnoyarsk State Technical University, Russia, 1999);
· I.V. Karlin, Method of invariant manifold in physical kinetics, (PhD, Physics, Krasnoyarsk AMSE Centre, Russia-France, 1991);
· V.I. Verbitsky, Simultaneously dissipative operators and global stability (PhD=“kandidat nauk”, Mathematical Analysis, Ural University, Yekaterinburg, Russia, 1989);
· M.G. Sadovskii, Optimization in space distributions of populations, (PhD=“kandidat nauk”, Biophysics, Institute of Biophysics, Russian Academy of Sciences, Krasnoyarsk, Russia, 1989);
· V.A. Okhonin, Kinetic equations for population dynamics (PhD=“kandidat nauk”, Biophysics, Moscow University, Russia, 1986).
Some latest achievement (2011-2016)
- Measure concentration effects in high-dimensional machine learning are analysed. In particular, it is showed that in high dimensions exponentially large number of randomly and independently chosen vectors are all pairwise almost orthogonal with probability close to one. These results imply the ‘uncertainty relations’: the approximation in random bases either requires exponentially long time or is ill-conditioned.
- New methods are developed for handling of missed data in large datasets and applied for analysis of the unknown trauma outcomes in the Trauma Audit and Research Network (TARN) database, the largest trauma database in Europe. The mortality numbers are corrected: Two naïve approaches give 7.20% (available case study) or 6.36% (if we assume that all unknown outcomes are ‘alive’). The corrected value is 6.78%. The approach developed can be applied to various healthcare datasets which experience the problem of lost patients and missed outcomes.
- A hierarchy of dynamic models of adaptation is developed based on formalization of Selye׳s ideas about adaptation energy and dynamics of adaptation. On the basis of these models, the phenomena of ‘oscillating death’ and ‘oscillating remission’ are predicted.
- The most general ordering of the distribution space, with respect to which all continuous-time Markov processes are monotonic (the Markov order) is introduces and analysed. For inference, this approach results in a set of conditionally “most random” distributions. Each distribution from this set is a maximizer of its own entropy. This “uncertainty of uncertainty” is unavoidable in the analysis of non-equilibrium systems. The constructive description of this set of maximizers is developed.
- Dynamical switching between phenotypic forms (or ‘phases’) of Streptococcus pneumoniae (the pneumococcus, which is the world’s foremost bacterial pathogen) is analysed in interaction with a large group of biologists. The underlying genetic mechanism for such phase variation is deciphered. Similar systems exist in other bacterial genera, indicating the potential for broad exploitation of epigenetic gene regulation.
- The space of admissible paths is analysed for the classes of dynamical systems, which are given in a positively invariant convex polyhedron D and have a given convex Lyapunov function. The problem of existence of admissible paths between states is solved constructively. The regions attainable by the admissible paths are constructively described.
- MicroRNAs (miRNAs) are key regulators of all important biological processes, including development, differentiation, and cancer. A mathematical model that combines nine known mechanisms of miRNA action is created. A computational tool for discriminating among different possible individual mechanisms of miRNA action based on translation kinetics data that is developed (kinetic signatures).
- For many complex real physicochemical
systems, the detailed mechanism includes both reversible and irreversible
reactions. Classical thermodynamics has no limit for irreversible
reactions, whereas kinetic equations may have such a limit. Systems with irreversible
reactions are analysed as the limits of fully reversible systems. If the
reversible systems obey the principle of detailed balance then the limit
system with some irreversible reactions must satisfy the extended
principle of detailed balance. It is formulated and proven in the form of
two conditions:
(i) the reversible part satisfies the principle of detailed balance and
(ii) the convex hull of the stoichiometric vectors of the irreversible reactions does not intersect the linear span of the stoichiometric vectors of the reversible reactions.
These conditions imply the existence of the global Lyapunov functionals and allow an algebraic description of the limit behaviour. - To solve the stability problem for lattice Boltzmann methods in modelling of highly non-equilibrium fluxes we develop new filtering techniques with independent filtering of different modes. The newly created limiters, which filter the modes independently, pick a reasonable value of the Reynolds number for the first bifurcation in the benchmark flows.
- .The theory of quasichemical models of multicomponent nonlinear diffusion is developed. The conditions thermodynamically correct behaviour are proven and the Lyapunov functional are found.
Some life-long scientific achievements:
- Kinetics.
A. Gorban has developed a family of methods for model reduction and coarse-graining: method of invariant manifold, method of natural projector, relaxation methods. He has solved problems in gas kinetics, polymer dynamics, chemical reaction kinetics and biological kinetics [1]. In recognition of this series of work, he received the I. Prigogine award and medal, has been a Clay Scholar (Cambridge, MA, USA, 2000), received Fellowship of I. Newton Institute (Cambridge, UK) and . Lifetime Achievement Award in recognition of outstanding contributions to the research field of (bio)chemical kinetics, MaCKIE-2015, Mathematics in (bio)Chemical Kinetics and Engineering, Ghent, Belgium, 2015.
- Solution of Hilbert problem
A. Gorban, with his student Karlin, have recently received the recognition of the scientific community [2,3] for solving an important part of the Hilbert 6th problem. This concerned the irreducibility of continuum mechanics to physical kinetics, a problem that remained unsolved for almost 100 years [4,5].
- The crises anticipation
A. Gorban invented a new method to measure stress caused by environmental factors. In particular, it appears possible to measure the ‘health’ of groups of healthy people [14]. This method is based on a universal effect discovered by A. Gorban in his study of human adaptation. This effect is supported by hundreds of experiments and observations and extended to systems of varying nature. Now, this method is used for the monitoring of Far North populations [15], for analysis of crises in national financial systems [16] and in companies [17]. It has become a part of the modern approach to crises anticipation [18].
Adaptation energy and oscillating death
• Stable Lattice Boltzmann methods
A new family of numerical methods is developed. They are based on the ideas of lattice Boltzmann models (LBM) in combination with methods of invariant manifold and specific entropic stabilisers. Standard test examples demonstrate that the new methods erase spurious oscillations without blurring of shocks, and do not affect smooth solutions [6,7].
- Bioinformatics
The methods of genome analysis based on frequency dictionaries are elaborated and applied to various biological problems (genome redundancy, mosaic structure of genome, genetic species signature, etc.). For example, existence of a universal 7cluster structure in all available bacterial genomes is proved [8,9].
- Data mining and rules extraction
A general neural networks based technology of extraction of explicit knowledge from data was developed. This technology was implemented in a series of software libraries and allowed A. Gorban and his team to create dozens of knowledge-based expert systems in medical and technical diagnosis, ecology and other fields. For example, new tools were developed for differential diagnosis of allergic and pseudoallergic reactions, for anticipation of myocardial infarction complications, and for evaluation of the accumulated radiation dose based on parameters of human blood [10].
- Revealing and visualizing the hidden structure of complex systems
A system of methods is developed to reveal the hidden intelligible models in complex systems: complex datasets and complex reaction networks [11,12]. This is revealing of hidden geometry. New special tools have been proposed and elaborated, such as the grammars of elementary transformations, which allow us to create the intelligible models of complex systems by the chains of simple steps and dominant systems that represent the complex networks by the simple networks, with dynamics that can be studied analytically. Several biological and medical centres now use these methods and algorithms, for example, Institute Curie (France).
- MicroRNAs kinetic signatures
MicroRNAs are key regulators of all important biological processes, including development, differentiation and cancer. Although remarkable progress has been made in deciphering the mechanisms used by miRNAs to regulate translation, many contradictory findings have been published that stimulate active debate in this field. A. Gorban, with co-authors, developed [13] computational tools for discriminating among different possible individual mechanisms of miRNA action, based on translation kinetics data that can be experimentally measured (kinetic signatures). They have found sensitive parameters of the translation process for various conditions.
- Neuroinformatics
In 1986, the duality principle was elaborated for training of very general networks. This principle is the maximally general form of the back-propagation algorithm, published independently in 1986 by the Rummelhat-Hinton team. The more general duality principle allowed the training of recurrent networks, networks from complex neurons described by integro-differential equations, etc. During four years of intensive work we have accelerated the training rate by several orders of magnitude using several approaches:
(1) Structurization of the space of the problems and skills.
(2) Employment of the modern methods of fast optimization.
(3) Modification of the target (utility) functions and several other technical improvements.
An essential part of these achievements was included in the book ‘Training of neural networks / USSR-USA JV ParaGraph’ [19]. In particular, it includes description of a simple method of virtual “particles” (neural agents) used for acceleration of learning (optimization of the utility function).
In the following 12 years, several generations of fast learning algorithms have been developed and implemented in several libraries of applied software. Many applied problems (dozens) have been solved, from medical and technical diagnosis to geoinformatics and data maps. The results are presented in books [19,10] and many papers. The software was transferred to hundreds of end users (with support) and was used in many projects. The prototype of this technology, which was later named "deep learning", was then developed.
In 1991, A. Gorban proposed a system of multi-agent neural intelligence based on the decomposition of the problem space due to cooperation and concurrency of agents. The interaction between agents was also managed by a special neural network [20].
[1] Gorban, A.N.; Karlin, I.V.; Zinovyev, A.Y., Constructive methods of invariant manifolds for kinetic problems, Physics Reports, 396, 2004, 197-403.
[2] Slemrod, M., From Boltzmann to Euler: Hilbert’s 6th problem revisited, Computers & Mathematics with Applications, 2012, http:// dx.doi.org/10.1016/j.camwa.2012.08.016.
[3] Slemrod, M., Chapman-Enskog → viscosity-capillarity, Quart. Appl. Math. 70 (2012), 613-624. [4] Gorban, A.N.; Karlin, I.V., Short-Wave Limit of Hydrodynamics: A Soluble Example, Physical Review Letters 77 (2), 282-285.
[5] Gorban, A.N.; Karlin, I., Hilbert's 6th Problem: exact and approximate hydrodynamic ma+nifolds for kinetic equations, Bulletin of the American Mathematical Society, 51(2), 2014, 186-246.
[6] Brownlee, R. A.; Gorban, A. N.; Levesley, J., Stability and stabilization of the lattice Boltzmann method, Phys. Rev. E 75, 036711 (2007)
[7] Brownlee, R. A.; Gorban, A. N.; Levesley, J., Nonequilibrium entropy limiters in lattice Boltzmann methods, Physica A 387(2-3) (2008), 385-406.
[8] Gorban, A.N.; Popova, T.; Zinovyev, A., Codon usage trajectories and 7-cluster structure of 143 complete bacterial genomic sequences, Physica A 353C (2005), 365-387.
[9] Gorban, A.N. ; Zinovyev, A.Y., The Mystery of Two Straight Lines in Bacterial Genome Statistics, Bulletin of Mathematical Biology 69 (2007), 2429–2442
[10] Gorban, A.N.; Rossiev, D.A., Neural networks on personal computer, Novosibirsk: Nauka, 1996, 276 pp. [In Russian]
[11] Gorban, A.N.; Kegl, B.; Wunsch, D. ; Zinovyev, A., Principal Manifolds for Data Visualisation and Dimension Reduction, Lecture Notes in Computational Science and Engineering, Vol. 58, Springer, Berlin – Heidelberg – New York, 2007.
[12] Gorban, A. N.; Radulescu, O.; Zinovyev, A.Y., Asymptotology of chemical reaction networks, Chemical Engineering Science 65 (2010) 2310–2324.
[13] Morozova, N.; Zinovyev, A.; Nonne, N.; Pritchard, L.-L.; Gorban, A.N.; and Harel-Bellan, A., Kinetic signatures of microRNA modes of action, RNA 18 (9) (2012), 1635-1655.
[14] Gorban, A.N.; Smirnova, E.V., Tyukina, T.A., Correlations, risk and crisis: From physiology to finance, Physica A 389 (16) (2010) 3193-3217.
[15] Sedov, K.R.; Gorban', A.N.; Petushkova (Smirnova), E.V.; Manchuk, V.T.; Shalamova, E.N., Correlation adaptometry as a method of screening of the population, Vestn. Akad. Med. Nauk SSSR (10) (1988) 69-75 [In Russian]
[16] Pokidysheva E.V., An Estimation of conjugacy of monetary and banking policy during crisis, Finance and credit 42(426) (2010), 72-78. [In Russian]
[17] Masaev, S.N.; Dorrer, M.G., Company management system evaluation on the basis of adaptive correlation to the environment, Control Sciences 2010, N 3, 45-50. [In Russian]
[18] Scheffer, M.; Carpenter, S.R.; Lenton, T.M.; Bascompte, J.; Brock, W.; Dakos, V.; van de Koppel, J.; van de Leemput, I.A.; Levin, S.A.; van Nes, E.H.; Pascual, M.; Vandermeer, J., Anticipating critical transitions, Science. 19, 338(6105) (2012), 344-348.
[19] Gorban A.N. Training of neural networks / USSR-USA JV ParaGraph, 1990.
[20] Gilev S.E., Gorban A.N., Mirkes E.M. Small experts and internal conflicts in artificial neural networks, Proc. of the USSR Academy of Sciences ("Doclady"), 1991. V.320, N.1. p.220-223.
Organizer of:
· International Research Workshop: Hilbert’s Sixth Problem, University of Leicester, Leicester, UK, May 2 – May 4, 2016.
· International Research Workshop: Coping with Complexity: Model Reduction and Data Analysis, Ambleside, Lake District, UK August 31 – September 4, 2009.
· International Research workshop: Mathematics of Model Reduction, University of Leicester, Leicester, UK August 28 – August 30, 2007,
· International Research Workshop: Lattice Boltzmann at all-scales: from turbulence to DNA translocation, 15 November 2006, University of Leicester, Leicester, UK,
· International Research Workshop: “Principal manifolds for data cartography and dimension reduction” August 24-26, 2006, Leicester University, Leicester, UK
· International Research Workshop: “Geometry of Genome: Unravelling of Structures Hidden in Genomic Sequences,” Leicester University, Leicester, UK, 22/09/2005 – 24/09/2005;
· International Research Workshop: “Model Reduction and Coarse-Graining Approaches for Multiscale Phenomena,” Leicester University, Leicester, UK August 24-26 2005;
· International Research Workshop: "Invariance and Model Reduction for Multiscale Phenomena," Zurich, August, 2003;
· USA-NIS Neurocomputing Opportunities Workshop, Washington, DC, July 1999, (Sponsored by the National Science Foundation of the USA and Applied Computational Intelligence Lab, TTU) (Co-Chair);
· Russian annual National Conference “Neurionformatics” (1998-present);
· Russian annual National Workshops “Neuroinformatics and Application,” Krasnoyarsk, 1992- present;
· Russian annual National Workshops “Modeling of Nonequilibrium Systems,” Krasnoyarsk, 1999- present.
· Russian National Conference “Problems of Regional Informatization”, Krasnoyarsk, 1998-2003.
· Soviet Union National competition in Neuroinformatics and Neurocomputers for students and young scientists, 1991.
Positive Media Coverage (Selected)
QuantaMagazine, July
21, 2015
Famous
Fluid Equations Are Incomplete
A 115-year effort to bridge the particle and fluid descriptions of nature
has led mathematicians to an unexpected answer.
Press Release in EurecAlert
Press Releases in ScienceDaily:
- New capillarity effects in ideal gases solve an old mathematical mystery (November 24, 2016)
- New approach for screening toxic chemicals mimics mammal senses (10 October 2016).
- Trauma patient deaths peak at two weeks (September 2, 2016)
- 'Adaptation energy' in animals: Mathematicians provide solution to 78 year old mystery (March 22, 2016)
- Breakthrough study discovers six changing faces of 'global killer' bacteria (September 30, 2014)
- New hope for beloved family pets: New blood test for canine cancer (September 23, 2014)
- Mathematicians solve decade-old debate on regulation of protein production by microRNAs in cells (July 31, 2012)
- Plants and animals under stress may provide the key to better stock market predications (Nov. 3, 2010)
Selected Publications
Monographs (in reverse chronological order):
- A.N. Gorban, D Roose (Eds) Coping with Complexity: Model Reduction and Data Analysis (Lecture Notes in Computational Science and Engineering, Springer, 2010.
- A.N. Gorban, B. Kegl, D. Wunsch, A. Zinovyev (Eds.), Principal Manifolds for Data Visualisation and Dimension Reduction, LNCSE 58, Springer, Berlin – Heidelberg – New York, 2007.
- A. N. Gorban, N. Kazantzis, I. G. Kevrekidis, H. C. Öttinger, C. Theodoropoulos (Eds.), Model Reduction and Coarse--Graining Approaches for Multiscale Phenomena, Springer, Berlin-Heidelberg-New York, 2006.
- A.N. Gorban, B.M. Kaganovich, S.P. Filippov, A.V. Keiko, V.A. Shamansky, I.A. Shirkalin, Thermodynamic Equilibria and Extrema: Analysis of Attainability Regions and Partial Equilibria, Springer, Berlin-Heidelberg-New York, 2006.
- A.N. Gorban, I.V. Karlin, Invariant Manifolds for Physical and Chemical Kinetics, Lect. Notes Phys. 660, Springer, Berlin, Heidelberg, 2005 (498 pages). [Review in Bull. London Math. Soc. 38 (2006)];
- A.N. Gorban, Singularities of transition processes in dynamical systems: Qualitative theory of critical delays, Electron. J. Diff. Eqns., Monograph 05, 2004, (55 pages). Online: http://ejde.math.unt.edu/Monographs/05/gorban.pdf
- A.N.Gorban, W.L.Dunin-Barkovskii, D.A.Rossiev, S.A.Terehov, Neuroinformatics, Novosibirsk, Nauka Publ., 1998, 258 p. (With W.L.Dunin-Barkovskii, D.A.Rossiev, S.A.Terehov). [In Russian]
- A.N.Gorban, D.A.Rossiev, Neural networks on PC, Novosibirsk, Nauka Publ., 1996, 276 p. (With D.A.Rossiev). [In Russian];
9. G.S.Yablonskii, V.I.Bykov, A.N.Gorban, V.I.Elokhin, Kinetic Models of Catalytic Reactions (Comprehensive Chemical Kinetics, V.32, ed. by R.G. Compton), Elsevier, Amsterdam, 1991, 396p. (Review on this book: Journal of American Chemical Society (JAChS), V.114, n 13, 1992; sections “Reviews on the book”, W. Henry Weinberg, review on the book "Comprehensive Chemical Kinetics", Volume 32, Kinetic Models of Catalytic Reactions, Elsevier, 1991).
- A.N. Gorban, Training of Neural Networks, Moscow, USSR-USA JV "ParaGraph", 1990, 160 p. [In Russian, Russian title “Obuchenie neironnyh setei”]
- A.N. Gorban, R.G.Khlebopros, Demon of Darwin. The Idea of Optimality and Natural Selection, Nauka Pub., Moscow, 1988, 208p. [In Russian]
- A.N. Gorban, V.I.Bykov, G.S.Yablonskii, Essays on Chemical relaxation, Novosibirsk, Nauka Publ., 1986, 316 p. [In Russian]
- A.N. Gorban, Equilibrium Encircling. Equations of Chemical Kinetics and their Thermodynamic Analysis, Novosibirsk, Nauka Publ., 1984, 256 p. [In Russian];
- G.S.Yablonskii, V.I.Bykov, A.N. Gorban, Kinetic models of heterogeneous catalytic reactions, Novosibirsk, Nauka Publ., 1983, 256 p. [In Russian].
Selected papers in peer-reviewed publications (in reverse chronological order). Impact Factor (IF) and rank of Journals in Quartiles for papers 2011-2016 are shown according to Thomson Reuters InCitesTM Journal Citation Report 2014,2015:
1. A.N. Gorban, I.V. Karlin, Beyond Navier–Stokes equations: capillarity of ideal gas, Contemporary Physics 58(1) (2017), 70-90, arXiv e-print. IF 5.0, Q1 IN PHYSICS, MULTIDISCIPLINARY
2. E. Moczko, E.M. Mirkes, C. Cáceres, A.N. Gorban, S. Piletsky, Fluorescence-based assay as a new screening tool for toxic chemicals, Scientific Reports 6, (2016) Article number: 33922. IF 5.228, Q1 IN INTERDISCIPLINARY SCIENCES
3. A.N. Gorban, E.M. Mirkes, A. Zinovyev, Piece-wise quadratic approximations of arbitrary error functions for fast and robust machine learning, Neural Networks, Volume 84, December 2016, 28-38 IF 3.216, Q1 IN COMPUTER SCIENCE, ARTIFICIAL INTELLIGENCE
4. E.M. Mirkes, T.J. Coats, J. Levesley, A.N. Gorban, Handling missing data in large healthcare dataset: a case study of unknown trauma outcomes, Computers in Biology and Medicine 75 (2016), 203-216. IF(2015) 1.521, Q2 IN MATHEMATICAL & COMPUTATIONAL BIOLOGY
5. A.N. Gorban, T.A. Tyukina, E.V. Smirnova, L.I. Pokidysheva, Evolution of adaptation mechanisms: Adaptation energy, stress, and oscillating death, Journal of Theoretical Biology 405 (2016), 127-139, IF(2014) 2.116; Q2 IN MATHEMATICAL & COMPUTATIONAL BIOLOGY
6. D.I. Iudin, I. Tyukin, A.N. Gorban, F.D. Iudin, V.B. Kazantsev, I.V. Muhina, T.T. Tyukina, Simple model of complex bursting dynamics in developing networks of neuronal cultures, IFAC-PapersOnLine. 2016 Dec 31;49(14):68-73.
7. E. Steur, I. Tyukin, A. N. Gorban, N. Jarman, H. Nijmeijer, and C. van Leeuwen. "Coupling-modulated multi-stability and coherent dynamics in directed networks of heterogeneous nonlinear oscillators with modular topology." IFAC-PapersOnLine 49, no. 14 (2016): 62-67.
8. A.A. Akinduko, E.M. Mirkes, A.N. Gorban SOM: Stochastic initialization versus principal components, Information Sciences (2016), Available online 27 October 2015, http://dx.doi.org/10.1016/j.ins.2015.10.013, IF(2014) 4.038, Q1 IN COMPUTER SCIENCE, INFORMATION SYSTEMS
9. A.N. Gorban, I.Yu. Tyukin, D.V. Prokhorov, K.I. Sofeikov Approximation with random bases: Pro et Contra Information Sciences 364–365 (2016), 129–145. IF(2014) 4.038, Q1 IN COMPUTER SCIENCE, INFORMATION SYSTEMS
10. A.N. Gorban, N. Jarman, E. Steur, H. Nijmeijer, C. van Leeuwen, I. Tyukin Directed cycles and multi-stability of coherent dynamics in systems of coupled nonlinear oscillators, IFAC-PapersOnLine, 48, (18) (2015), 19–24
11. A.N. Gorban , A. Zinovyev, Fast and user-friendly non-linear principal manifold learning by method of elastic maps, in Proceedings of DSAA 2015 -- IEEE International Conference on Data Science and Advanced Analytics, Paris; 10/2015.
12. A.N. Gorban, Forward-Invariant Peeling in Chemical Dynamics: a Simple Case Study, Mathematical Modelling of Natural Phenomena Vol. 10, No. 5, 2015, pp. 126–134. IF(2014) 0.813, Q2 IN ITERDISCIPLINARY SCIENCES
13. A.N. Gorban, V.N. Kolokoltsov, Generalized Mass Action Law and Thermodynamics of Nonlinear Markov Processes, Mathematical Modelling of Natural Phenomena Vol. 10, No. 5, 2015, pp. 16–46. IF(2014) 0.813, Q2 IN ITERDISCIPLINARY SCIENCES
14. A.N. Gorban, N. Jarman, E. Steur, C. van Leeuwen, I.Yu. Tyukin, Leaders Do Not Look Back, or Do They? Mathematical Modelling of Natural Phenomena Vol. 10, No. 3, 2015, pp. 212–231. IF(2014) 0.813, Q2 IN ITERDISCIPLINARY SCIENCES
15. A.N. Gorban, I.Yu. Tyukin, H. Nijmeijer, Further Results on Lyapunov-Like Conditions of Forward Invariance and Boundedness for a Class of Unstable Systems, in Proceedings of 53rd IEEE Conference on Decision and Control December 15-17, 2014. Los Angeles, California, USA, IEEE, 2014, pp. 1557-1562
16. A.S. Manso, M.H. Chai, J.M. Atack, L. Furi, M. De Ste Croix, R. Haigh, C. Trappetti, A.D. Ogunniyi, L.K. Shewell, M. Boitano, T.A. Clark, J. Korlach, M. Blades, E. Mirkes, A.N. Gorban, J.C. Paton, M.P. Jennings, M.R. Oggioni, A random six-phase switch regulates pneumococcal virulence via global epigenetic changes, Nature Communications 5 (2014), Article number: 5055. IF(2014), 11.470, Q1 IN ITERDISCIPLINARY SCIENCES
17. E.M. Mirkes, I. Alexandrakis, K. Slater, R. Tuli, A.N. Gorban, Computational diagnosis and risk evaluation for canine lymphoma, Computers in Biology and Medicine, Volume 53, 1 October 2014, 279-290. IF(2014) 1.240, Q3 IN MATHEMATICAL & COMPUTATIONAL BIOLOGY
18. A.N. Gorban, Detailed balance in micro- and macrokinetics and micro-distinguishability of macro-processes, Results in Physics, Volume 4, 2014, 142-147.
19. A.N. Gorban, D.J. Packwood, Enhancement of the stability of lattice Boltzmann methods by dissipation control, Physica A 414 (2014) 285–299. IF(2014) 1.732, Q2 IN PHYSICS, MULTIDISCIPLINARY
20. A.N. Gorban, General H-theorem and Entropies that Violate the Second Law. Entropy 2014, 16, 2408-2432. IF(2014) 1.502, Q2 IN PHYSICS, MULTIDISCIPLINARY
21. A.N. Gorban, I. Karlin, Hilbert's 6th Problem: exact and approximate hydrodynamic manifolds for kinetic equations, Bulletin of the American Mathematical Society 51(2), 2014, 186-246. IF(2014) 2.107, Q1 IN MATHEMATICS
22.
Spahn, F., Vieira
Neto, E., Guimarães, A.H.F., Gorban, A.N., Brilliantov, N.V.
A statistical model of aggregate
fragmentation, New Journal of Physics
16, Article number 013031, 2014. IF(2014) 3.558, Q1 IN PHYSICS, MULTIDISCIPLINARY
23. E M Mirkes, I Alexandrakis, K Slater, R Tuli and A N Gorban, Computational diagnosis of canine lymphoma, J. Phys.: Conf. Ser. 490 012135 (2014)
24. A A Akinduko and A N Gorban, Multiscale principal component analysis, J. Phys.: Conf. Ser. 490 012081 (2014)
25. Y Shi, A N Gorban and T Y Yang, Is it possible to predict long-term success with k-NN? Case study of four market indices (FTSE100, DAX, HANGSENG, NASDAQ), J. Phys.: Conf. Ser. 490 012082 (2014)
26. K.I. Sofeikov, I. Romanenko, I. Tyukin, A.N. Gorban, Scene Analysis Assisting for AWB Using Binary Decision Trees and Average Image Metrics. In Proceedings of IEEE Conference on Consumer Electronics, 10-13 January, Las-Vegas, USA, 2014, pp. 488-491.
27. A.N. Gorban, I. Tyukin, E. Steur, and H. Nijmeijer, Lyapunov-like conditions of forward invariance and boundedness for a class of unstable systems, SIAM Journal On Control And Optimization Vol. 51, No. 3, 2013, pp. 2306-2334. IF(2014) 1.463, Q1 IN MATHEMATICS, APPLIED
22. E.M. Mirkes, A. Zinovyev, and A.N. Gorban, Geometrical Complexity of Data Approximators, in I. Rojas, G. Joya, and J. Cabestany (Eds.): IWANN 2013, Part I, Advances in Computation Intelligence, Springer LNCS 7902, pp. 500–509, 2013.
23. A.N. Gorban, G.S. Yablonsky, Grasping Complexity, Computers & Mathematics with Applications, Volume 65, Issue 10, May 2013, 1421-1426. IF(2014) 1.697, Q1 IN MATHEMATICS, APPLIED
24. R.A. Brownlee, J. Levesley, D. Packwood, A.N. Gorban, Add-ons for Lattice Boltzmann Methods: Regularization, Filtering and Limiters, Progress in Computational Physics, 2013, vol. 3, 31-52.
25. A.N. Gorban, Maxallent: Maximizers of all entropies and uncertainty of uncertainty, Computers & Mathematics with Applications 65, Issue 10, May 2013, 1438-1456. IF(2014) 1.697, Q1 IN MATHEMATICS, APPLIED
26. A. N. Gorban, Thermodynamic Tree: The Space of Admissible Paths, SIAM Journal On Applied Dynamical Systems, Vol. 12, No. 1 (2013), pp. 246-278. IF(2014) 1.439, Q1 IN MATHEMATICS, APPLIED
27. A. Zinovyev, N. Morozova, A.N. Gorban, and A. Harel-Belan, Mathematical Modeling of microRNA-Mediated Mechanisms of Translation Repression, in U. Schmitz et al. (eds.), MicroRNA Cancer Regulation: Advanced Concepts, Bioinformatics and Systems Biology Tools, Advances in Experimental Medicine and Biology Vol. 774, Springer, 2013, pp. 189-224. IF(2014) 1.958, Q2 IN BIOLOGY
28. A.N. Gorban, E.M. Mirkes, G.S. Yablonsky Thermodynamics in the limit of irreversible reactions, Physica A 392 (2013) 1318–1335. IF(2014) 1.732, Q2 IN PHYSICS, MULTIDISCIPLINARY
29. A.N. Gorban, Local equivalence of reversible and general Markov kinetics, Physica A 392 (2013) 1111–1121. IF(2014) 1.732, Q2 IN PHYSICS, MULTIDISCIPLINARY
30. A.N. Gorban and D. Packwood, Allowed and forbidden regimes of entropy balance in lattice Boltzmann collisions, Physical Review E 86, 025701(R) (2012). IF(2014) 2.288, Q1 IN PHYSICS, MATHEMATICAL
31. N. Morozova, A. Zinovyev, N. Nonne, L.-L. Pritchard, A.N. Gorban, and A. Harel-Bellan, Kinetic signatures of microRNA modes of action, RNA-A Publication of the RNA Society, Vol. 18, No. 9 (2012), 1635-1655. IF(2014) 4.962, Q1 IN BIOCHEMISTRY AND MOLECULAR BIOLOGY
32. A.N. Gorban, G.S.Yablonsky, Extended detailed balance for systems with irreversible reactions, Chemical Engineering Science 66 (2011) 5388–5399. IF(2014) 2.337, Q2 IN ENGINEERING, CHEMICAL
33. A.N. Gorban, H.P. Sargsyan and H.A. Wahab, Quasichemical Models of Multicomponent Nonlinear Diffusion, Mathematical Modelling of Natural Phenomena, Volume 6 / Issue 05, (2011), 184−262. IF(2014) 0.813, Q2 IN ITERDISCIPLINARY SCIENCES
34. G. S. Yablonsky, A. N. Gorban, D. Constales, V. V. Galvita and G. B. Marin, Reciprocal relations between kinetic curves, EPL, 93 (2011) 20004. IF(2014) 2.095, Q2 IN PHYSICS, MULTIDISCIPLINARY
35. A.N. Gorban and M. Shahzad, The Michaelis-Menten-Stueckelberg Theorem. Entropy 2011, 13, 966-1019. IF(2014) 1.502, Q2 IN PHYSICS, MULTIDISCIPLINARY
36. A.N. Gorban, Kinetic path summation, multi-sheeted extension of master equation, and evaluation of ergodicity coefficient, Physica A 390 (2011) 1009–1025. IF(2014) 1.732, Q2 IN PHYSICS, MULTIDISCIPLINARY
37. A.N. Gorban, L.I. Pokidysheva, E,V. Smirnova, T.A. Tyukina. Law of the Minimum Paradoxes, Bulletin of Mathematical Biology 73(9) (2011), 2013-2044. IF(2014) 1.389, Q3 IN MATHEMATICAL & COMPUTATIONAL BIOLOGY
38. A. Gorban and S. Petrovskii, Collective dynamics: when one plus one does not make two, Mathematical Medicine and Biology-A Journal of the IMA (2011) 28, 85−88. IF(2014) IF 1.658, Q2 IN MATHEMATICAL & COMPUTATIONAL BIOLOGY
39. A.N. Gorban, E.V. Smirnova, T.A. Tyukina, Correlations, risk and crisis: From physiology to finance, Physica A, Vol. 389, Issue 16, 2010, 3193-3217.
40. A. N. Gorban, A. Zinovyev. Principal manifolds and graphs in practice: from molecular biology to dynamical systems, International Journal of Neural Systems, Vol. 20, No. 3 (2010) 219–232.
41. E. Chiavazzo, I.V. Karlin, A.N. Gorban, K. Boulouchos, Coupling of the model reduction technique with the lattice Boltzmann method, Combustion and Flame, 2010
42. Gorban A.N., Gorban P.A., Judge G. Entropy: The Markov Ordering Approach. Entropy. 2010; 12(5):1145-1193
43. A. N. Gorban and V. M. Cheresiz, Slow Relaxations and Bifurcations of the Limit Sets of Dynamical Systems. I. Bifurcations of Limit Sets, Journal of Applied and Industrial Mathematics, 2010, Vol. 4, No. 1, pp. 54–64.
44. A. N. Gorban and V. M. Cheresiz, Slow Relaxations and Bifurcations of the Limit Sets of Dynamical Systems. II. Slow Relaxations of a Family of Semiflows, Journal of Applied and Industrial Mathematics, 2010, Vol. 4, No. 2, pp. 182–190.
45. E. Chiavazzo, I.V. Karlin, and A.N. Gorban, The Role of Thermodynamics in Model Reduction when Using Invariant Grids, Commun. Comput. Phys., Vol. 8, No. 4 (2010), pp. 701-734.
46. Andrei Zinovyev, Nadya Morozova, Nora Nonne, Emmanuel Barillot, Annick Harel-Bellan, Alexander N Gorban, Dynamical modeling of microRNA action on the protein translation process, BMC Systems Biology 2010, 4:13 (24 February 2010)
47. A. N. Gorban, O. Radulescu, A. Y. Zinovyev, Asymptotology of chemical reaction networks, Chemical Engineering Science 65 (2010) 2310–2324
48. A.N. Gorban, E.V. Smirnova, T.A. Tyukina, General Laws of Adaptation to Environmental Factors: from Ecological Stress to Financial Crisis. Math. Model. Nat. Phenom. Vol. 4, No. 6, 2009, pp. 1-53
49. E. Chiavazzo, I. V. Karlin, A. N. Gorban and K Boulouchos, Combustion simulation via lattice Boltzmann and reduced chemical kinetics, J. Stat. Mech. (2009) P06013,
50. Ovidiu Radulescu, Alexander N Gorban, Andrei Zinovyev, and Alain Lilienbaum, Robust simplifications of multiscale biochemical networks, BMC Systems Biology 2008, 2:86
51. A.N. Gorban and O. Radulescu, Dynamic and Static Limitation in Multiscale Reaction Networks, Revisited, Advances in Chemical Engineering 34, 103-173.
52. R. A. Brownlee, A. N. Gorban, and J. Levesley, Nonequilibrium entropy limiters in lattice Boltzmann methods, Physica A, 387 (2-3) (2008), 385-406
53. A.N. Gorban and O. Radulescu, Dynamical robustness of biological networks with hierarchical distribution of time scales, IET Syst. Biol., 1, (4) (2007), 238–246
54. A.N. Gorban and A.Y. Zinovyev, The Mystery of Two Straight Lines in Bacterial Genome Statistics, Bulletin of Mathematical Biology 69 (2007), 2429–2442.
55. R. A. Brownlee, A. N. Gorban, and J. Levesley, Stability and stabilization of the lattice Boltzmann method, Phys. Rev. E 75, 036711 (2007) (17 pages)
56. E. Chiavazzo, A.N. Gorban, and I.V. Karlin, Comparison of Invariant Manifolds for Model Reduction in Chemical Kinetics, Commun. Comput. Phys. Vol. 2, No. 5 (2007), pp. 964-992
57. A.N. Gorban, N.R. Sumner, and A.Y. Zinovyev, Topological grammars for data approximation, Applied Mathematics Letters Volume 20, Issue 4 (2007), 382-386
58. A.N. Gorban, Order–disorder separation: Geometric revision, Physica A 374 (1), (2007), 85-102
59. R.A. Brownlee, A.N. Gorban, and J. Levesley, Stabilization of the lattice Boltzmann method using the Ehrenfests' coarse-graining idea, Phys. Rev. E 74, 037703 (2006)
60. A. Gorban, I. Karlin, A. Zinovyev, Invariant Grids: Method of Complexity Reduction in Reaction Networks, Complexus, V. 2, 110–127.
61. A.N. Gorban, I.V. Karlin, Quasi-Equilibrium Closure Hierarchies for the Boltzmann Equation, Physica A 360 (2006) 325–364
62. A. Gorban, A. Zinovyev, Elastic Principal Graphs and Manifolds and their Practical Applications, Computing 75, 359–379 (2005),
63. A.N. Gorban, I.V. Karlin, Invariance correction to Grad's equations: Where to go beyond approximations? Continuum Mechanics and Thermodynamics, 17(4) (2005), 311–335,
64. A.N. Gorban, T.G.Popova, A.Yu. Zinovyev, Codon usage trajectories and 7-cluster structure of 143 complete bacterial genomic sequences •Physica A: Statistical and Theoretical Physics, 353C (2005), 365-387.
65. A.N. Gorban, T.G.Popova, A.Yu. Zinovyev, Four basic symmetry types in the universal 7-cluster structure of microbial genomic sequences, In Silico Biology, 5 (2005), 0039.
66. A.N. Gorban, P.A.Gorban, and I. V. Karlin, Legendre Integrators, Post-Processing and Quasiequilibrium, J. Non-Newtonian Fluid Mech. 120 (2004) 149-167.
67. A.N. Gorban, I.V. Karlin, A.Yu. Zinovyev, Constructive methods of invariant manifolds for kinetic problems, Physics Reports, V. 396, N 4-6 (2004), p. 197-403.
68. A.N. Gorban, I.V. Karlin, A.Yu. Zinovyev, Invariant grids for reaction kinetics, Physica A, 333 (2004), 106--154.
69. A.N. Gorban, I.V. Karlin, Uniqueness of thermodynamic projector and kinetic basis of molecular individualism, Physica A, 336, 3-4 (2004), 391-432.
70. A.N. Gorban, T. G. Popova, and A. Yu. Zinovyev: Self-organizing approach for automated gene identification. Open Sys. Information Dyn. 10 (2003) 1-13.
71. A.N. Gorban and I. V. Karlin, Family of additive entropy functions out of thermodynamic limit, Phys. Rev. E. 2003, V.67, 016104, E-print: http:, arXiv.org/abs/cond-mat/0205511
72. A.N. Gorban, I. V. Karlin and H. C. Ottinger, The additive generalization of the Boltzmann entropy. Phys. Rev. E. (2003), V. 67. E-print: http:, arXiv.org/abs/cond-mat/0209319.
73. A.N. Gorban, I. V. Karlin, Method of invariant manifold for chemical kinetics. Chem. Eng. Sci. 58 (2003) 4751-4768.
74. I.V. Karlin, L. L. Tatarinova, A. N. Gorban, and H. C. Öttinger, Irreversibility in the short memory approximation, Physica A 327 (2003) 399-424.
75. A. Gorban, A. Zinovyev, T. Popova. Seven clusters in genomic triplet distributions. In Silico Biology. V.3 (2003), 471-482.
76. A.N. Gorban, T.G Popova, M.G Sadovsky, Classification of nucleotide sequences over their frequency dictionaries reveals a relation between the structure of sequences and taxonomy of their bearers, Zh Obshch Biol 64 (1), 65-77. 2003
77. A. Gorban', Braverman M., Silantyev V. Modified Kirchhoff flow with a partially penetrable obstacle and its application to the efficiency of free flow turbines. Math. Comput. Modelling 35 (2002), No. 13, 1371-1375.
78. A. Gorban', Silantyev V. Riabouchinsky Flow with Partially Penetrable Obstacle. Math. Comput. Modelling 35 (2002), no. 13, 1365-1370.
79. I.V. Karlin, M. Grmela, and A.N. Gorban: Duality in nonextensive statistical mechanics, Phys. Rev. E 65 (2002) 036128.
80. A.N. Gorban and I. V. Karlin, Reconstruction lemma and fluctuation-dissipation theorem, Revista Mexicana de Fisica, 2002. V. 48 Suplemento 1, PP. 238-242.
81. A.N. Gorban and I. V. Karlin, Geometry of irreversibility, in: Recent Developments in Mathematical and Experimental Physics, Volume C: Hydrodynamics and Dynamical Systems, Ed. F. Uribe (Kluwer, Dordrecht, 2002), pp. 19-43.
82. A.N. Gorban and I. V. Karlin, Macroscopic dynamics through coarse-graining: A solvable example, Phys. Rev. E. V 65. 026116(1-5) (2002).
83. I.V. Karlin and A.N. Gorban, Hydrodynamics from Grad's equations: What can we learn from exact solutions? Ann. Phys. (Leipzig) 10-11 (2002), pp. 783-833. E-print: http:, arXiv.org/abs/cond-mat/0209560
84. A.N. Gorban, Zinov'ev A.Y., Pitenko A.A., Data vizualization. The method of elastic maps, Neirocompjutery, 2002, 4, 19-30.
85. A.N. Gorban, A.A Rossiev, Iterative modeling of data with gaps via submanifolds of small dimension, Neirocompjutery, 2002, 4, 40-44.
86. A. Gorban, Rossiev A., Makarenko N., Kuandykov Y., Dergachev V. Recovering data gaps through neural network methods. International Journal of Geomagnetism and Aeronomy, 2002, Vol. 3, No. 2, December 2002.
87. A.N. Gorban, V.T. Manchuk, A.V.Perfil’eva, E.V.Smirnova, E.P. Cheusova, The mechanism of increasing the correlation between physiological parameters for high adaptation tension, Siberian Ecological Journal, 2001, No 5, 651-655.
88. A.N. Gorban, Gorlov A.M., Silantyev V.M. Limits of the turbin efficiency for free fluid flow, ASME Journal of Energy Resourses Technology, Dec. 2001, V. 123, Iss. 4, pp. 311-317.
89. A.N. Gorban, Pitenko A.A., Zinov'ev A.Y., Wunsch D.C. Vizualization of any data uzing elastic map method , Smart Engineering System Design. 2001, V.11, p. 363-368.
90. A.N. Gorban, Popova T.G., Sadovsky M.G., Wunsch D.C. Information content of the frequency dictionaries, reconstruction, transformation and classification of dictionaries and genetic texts. Smart Engineering System Design, 2001, V.11, p. 657-663.
91. A.N.Gorban, I.V.Karlin, P.Ilg and H.C.Ottinger Corrections and enhancements of quasi-equilibrium states, J. Non-Newtonian Fluid Mech., 2001, V.96(1-2), PP. 203-219.
92. A.N. Gorban, Karlin I.V., Ottinger H.C., Tatarinova L.L. Ehrenfest's argument extended to a formalism of nonequilibrium thermodynaics, Phys. Rev. E. 2001, V. 63. 066124.
93. A.N. Gorban, Gorbunova K.O., Wunsch D.C. Liquid Brain: The Proof of Algorithmic Universality of Quasichemical Model of Fine-Grained Parallelism, Neural Network World, 2001, No. 4. P P. 391-412.
94. A.N. Gorban, Zinovyev A. Yu. Method of Elastic Maps and its Applications in Data Visualization and Data Modeling. International Journal of Computing Anticipatory Systems, CHAOS. 2001. V. 12. PP. 353-369.
95. V.A. Dergachev, Gorban A.N., Rossiev A.A., Karimova L.M., Kuandykov E., Makarenko N.G., Steier. The filling of gaps in geophysical time series by artificial neural networks, Radiocarbon, 2001, V. 43, No. 2, PP. 343-348.
96. A.N.Gorban, V.P.Torchilin, M.V.Malyutov, M. Lu Modeling polymer brushes protective action , Simulation in Industry' 2000. Proceedings of 12-th European Simulation Symposium ESS'2000. September 28-30, 2000, Hamburg, Germany. A publication of the Society of Computer Simulation International. Printed in Delft, The Netherlands, 2000. PP. 651-655.
97. A.N.Gorban, Neuroinformatics: What are us, where are we going, how to measure our way? Informacionnye technologii, 2000, 4. - С. 10-14.
98. A.N. Gorban, K. O. Gorbunova, Liquid Brain: Kinetic Model of Structureless Parallelism, Internation Journal of Computing Anticipatory Systems, CHAOS, V. 6, 2000, P.117-126.
99. A.N. Gorban, I.V. Karlin, V.B. Zmievskii and S.V. Dymova, Reduced description in reaction kinetics, Physica A, 2000. V. 275, No. 3-4, PP. 361-379.
100. A.N Gorban, The generalized Stone approximation theorem for arbitrary algebras of continuous functions, Dokl Akad Nauk, 365 (5), 586-588, 1999
101. A.N. Gorban, A.A Rossiev, Neural network iterative method of principal curves for data with gaps, J Comput Sys Sc Int, 38 (5): 825-830, 1999.
102. A.N. Gorban, I.V.Karlin and V.B.Zmievskii, Two-step approximation of space-independent relaxation, Transp.Theory Stat.Phys., 1999. V. 28(3), PP. 271-296.
103. A.N. Gorban, Approximation of Continuous Functions of Several Variables by an Arbitrary Nonlinear Continuous Function of One Variable, Linear Functions, and Their Superpositions. Appl. Math. Lett., 1998. V. 11, No. 3, pp. 45-49.
104. S.E. Gilev, A.N. Gorban, The completeness theorem for semigroups of continuous functions, Dokl Akad Nauk, 362 (6): 733-734, 1998
105. N.N.Bugaenko, A. N. Gorban, M.G.Sadovskii, Maximum entropy method in analysis of genetic text and measurement of its information content , Open systems and information dynamics. No. 5, 1998. - pp.265-278.
106. A.N. Gorban, Neuroinformatics and applications, Otkrytye sistemy (Open Systems), 1998, No. 4-5. pp. 36-41.
107. A.N. Gorban, I.V. Karlin, Sroedinger operator in a overfull set , Europhys. Lett., 1998, V. 42, No.2, pp. 113-117.
108. I.V. Karlin, A. N. Gorban, S. Succi, V. Boffi, Maximum Entropy Principle for Lattice Kinetic Equation , Physical Review Letters, 1998, V. 81, No. 1, pp. 6-9.
109. A.N. Gorban, Yeugenii M. Mirkes and Donald Wunsch, High Order Orthogonal Tensor Networks: Information Capacity and Reliability, Proc. IEEE/INNS International Conference on Neural Networks, Houston, IEEE, 1997, pp. 1311-1314.
110. A.N. Gorban, Masha Yu. Senashova and Donald Wunsch, Back-Propagation of Accuracy, Proc. IEEE/INNS International Conference on Neural Networks, Houston, IEEE, 1997, pp. 1998-2001.
111. N.N. Bugaenko, A. N. Gorban, M.G.Sadovskii, Information content of nucleotid sequences and their fragments. Biofizika. 1997. V. 42, Iss. 5, pp. 1047-1053.
112. V.I. Bykov, A.N. Gorban, S.V. Dymova, Method of invariant manifolds for the reduction of kinetic description, ACH-Models Chem 134 (1): 83-95 1997
113. A.N. Gorban, I.V.Karlin, Scattering rates versus moments: Alternative Grad equations, Phys. Rev. E, 1996, 54(4), R3109.
114. A.N. Gorban, I.V.Karlin, Short-Wave Limit of Hydrodynamics: A Soluble Example, Phys. Rev. Lett., 1996, V. 77, N. 2, P. 282-285.
115. N.N. Bugaenko, A.N. Gorban, M.G. Sadovskii, Information content in nucleotide sequences, Mol Biol, 30 (3): 313-320, 1996.
116. A.N. Gorban, T.G. Popova, M.G. Sadovskii, Human virus genes are less redundant than human genes, Genetika, 32 (2), 289-294, 1996.
117. A.N. Gorban, I.V.Karlin, V.B.Zmievskii, T.F.Nonnenmacher, Relaxational trajectories: global approximations, Physica A, 1996, V.231, No.4, p.648-672.
118. A.N. Gorban, D.N.Golub, Multi-Particle Networks for Associative Memory, Proc. of the World Congress on Neural Networks, Sept. 15-18, 1996, San Diego, CA, Lawrence Erlbaum Associates, 1996, pp. 772-775.
119. S.E. Gilev, A. N. Gorban, On Completeness of the Class of Functions Computable by Neural Networks, Proc. of the World Congress on Neural Networks, Sept. 15-18, 1996, San Diego, CA, Lawrence Erlbaum Associates, 1996, pp. 984-991.
120. A.N. Gorban, D.A. Rossiyev, E.V. Butakova, S.E. Gilev, S.E. Golovenkin, S.A. Dogadin, D.A. Kochenov, E.V. Maslennikova, G.V. Matyushin, Y.E. Mirkes, B.V. Nazarov, Medical and Physiological Applications of MultiNeuron Neural Simulator. Proceedings of the 1995 World Congress On Neural Networks, A Volume in the INNS Series of Texts, Monographs, and Proceedings, Vol. 1, 1995.
121. M.G. Dorrer, A.N. Gorban, A.G. Kopytov, V.I. Zenkin, Psychological Intuition of Neural Networks. Proceedings of the 1995 World Congress On Neural Networks, A Volume in the INNS Series of Texts, Monographs, and Proceedings, Vol. 1, 1995.
122. A.N. Gorban, C. Waxman, Neural Networks for Political Forecast. Proceedings of the 1995 World Congress On Neural Networks, A Volume in the INNS Series of Texts, Monographs, and Proceedings, Vol. 1, 1995.
123. A.N. Gorban, T.G. Popova, M.G. Sadovskii, Redundancy of genetic texts, Mol Biol, 28 (2), 206-213, 1994.
124. A.N. Gorban, T.G. Popova, M.G. Sadovskii, Correlation approach to comparing nucleotide-sequences, Zh Obshch Biol, 55 (4-5), 420-430, 1994.
125. A.N. Gorban, I.V. Karlin, General approach to constructing models of the Boltzmann equation, Physica A, 206 (1994), 401-420.
126. A.N. Gorban, I.V. Karlin, Method of invariant manifolds and regularization of acoustic spectra, Transport Theory and Stat. Phys., 23, 559-632, 1994.
127. A.N. Gorban, E.M. Mirkes, T.G. Popova, M.G. Sadovskii, A new approach to the investigations of statistical properties of genetic texts, Biofizika 38 (5), 762-767, 1993.
128. A.N. Gorban, E.M. Mirkes, T.G. Popova, M.G. Sadovskii, The comparative redundancy of genes of various organisms and viruses, Genetika 29 (9), 1413-1419, 1993.
129. A.N. Gorban, I.V.Karlin, Structure and Approximations of the Chapman-Enskog Expansion for Linearized Grad Equations, Transport Theory and Stat.Phys, V.21, No 1&2, P.101-117, 1992.
130. V.I. Verbitskii, A.N. Gorban, Jointly dissipative operators and their applications, Siberian Math J, 33 (1), 19-23, 1992.
131. A.N. Gorban, E.M. Mirkes, A.P. Svitin, Method of multiplet covering and its application for the prediction of atom and molecular-properties, Zh Fiz Khim, 66 (6): 1504-1510, 1992.
132. V.I. Bykov, V.I. Verbitskii, A.N. Gorban, Evaluation of cauchy-problem solution with inaccurately given initial data and the right part, Izv Vuz Mat, (12), 5-8, 1991.
133. A.N. Gorban, V.I.Verbitsky, Simultaneously Dissipative Operators and Quasi-Thermodynamicity of the Chemical Reactions Systems, Advances in Modelling and Simulation, 1992, V.26, N1, p.13-21.
134. N.N. Bugaenko, A. N. Gorban, I.V.Karlin Universal Expansion of the Triplet Distribution Function, Teoreticheskaya i Matematicheskaya Fisica, V.88, No.3, P.430-441(1991).
135. A.N. Gorban, I.V.Karlin, Approximations of the Chapman-Enskog Expansion, Zh.Exp.Teor.Fis., V.100, No.4(10), P.1153-1161(1991); Sov. Phys. JETP, V.73(4), P.637-641.(1991).
136. S.Ye. Gilev, A. N. Gorban and E.M. Mirkes, Small Experts and Internal Conflicts in Learnable Neural Networks, Doklady Acad. Nauk SSSR, V.320, No.1, (1991) P.220-223.
137. A.N. Gorban, E.M. Mirkes, A.N. Bocharov, V.I. Bykov, Thermodynamic consistency of kinetic data, Combust Explosion & Shock, 25 (5), 593-600, 1989.
138. V.I. Verbitskii, A.N. Gorban, G.S. Utiubaev, Y.I. Shokin, Moores effect in interval spaces, Dokl Akad Nauk SSSR, 304 (1), 17-21 1989.
139. A.N. Gorban, M.G. Sadovskii, Optimal strategies of spatial-distribution - Olli effect, Zh Obshch Biol 50 (1), 16-21, 1989.
140. A.N. Gorban, K.R.Sedov and E.V.Smirnova, Correlation Adaptometry as a Method for Measuring the Health, Vestnik Acad. Medic. Nauk SSSR, No.5, P.69-75(1989).
141. V.I.Bykov, A. N. Gorban, A Model of Autooscillations in Association Reactions, Chem.Eng.Sci., V.42, No.5, P.1249-1251(1987).
142. A.N. Gorban, M.G.Sadovskii, Evolutionary Mechanisms of Creation of Cellular Clusters in Flowrate Cultivators, Biotechnology and Biotechnics, No.5, P.34-36(1987).
143. V.I.Bykov, A. N. Gorban, G.S.Yablonskii. Thermodynamic Function Analogue for Reactions Proceeding Without Interactions of Various Substances, Chem.Eng.Sci., V.41, No.11, P.2739-2745 (1986).
144. V.I. Bykov, S.E. Gilev, A.N. Gorban, G.S. Yablonskii, Imitation modeling of the diffusion on the surface of a catalyst, Dokl Akad Nauk SSSR, 283 (5): 1217-1220 1985.
145. V.I. Bykov, A.N. Gorban, Simplest model of self-oscillations in association reactions, React Kinet Catal Lett, 27 (1): 153-155 1985
146. V.I. Bykov, A.N. Gorban, T.P. Pushkareva, Autooscillation model in reactions of the association, Zh Fiz Khim, 59 (2): 486-488, 1985.
147. A.N. Gorban, V.I. Bykov, G.S. Yablonskii, Description of non-isothermal reactions using equations of nonideal chemical-kinetics, Kinet Catal, 24 (5), 1055-1063, 1983.
148. V.I. Bykov, A.N. Gorban, L.P. Kamenshchikov, G.S. Yablonskii, Inhomogeneous stationary states in reaction of carbon-monoxide oxidation on platinum, Kinet Catal, 24 (3), 520-524, 1983
149. V.I. Bykov, A.N. Gorban, Quasithermodynamic characteristic of reactions without the reaction of different substances, Zh Fiz Khim, 57 (12), 2942-2948, 1983.
150. V.I. Bykov, A.N. Gorban, G.S. Yablonskii, Description of non-isothermal reactions in terms of Marcelin-De-Donder kinetics and its generalizations, React Kinet Catal Lett, 20 (3-4), 261-265, 1982.
151. S.E. Gilev, A.N. Gorban, V.I. Bykov, G.S. Yablonskii, Simulative modeling of processes on a catalyst surface, Dokl Akad Nauk SSSR, 262 (6), 1413-1416, 1982.
152. V.I. Elokhin, G.S. Yablonskii, A.N. Gorban, V.M. Ceresiz, Dynamics of chemical-reactions and non-physical steady-states, React Kinet Catal Lett, 15 (2), 245-250, 1980.
153. A.N. Gorban, G.S. Yablonskii, On one unused possibility in the kinetic experiment design, Dokl Akad Nauk SSSR, 250 (5): 1171-1174, 1980.
154. A.N. Gorban, V.I. Bykov, G.S. Yablonskii, The Path to Equilibrium, Intern. Chem. Eng. V.22, No.2, P.386-375(1982).
155. A.N. Gorban, V.M.Ceresiz, Slow Relaxations of Dynamical Systems and Bifurcations of Omega-Limit Sets, Soviet Math. Dokl., V.24, P.645-649(1981).
156. A.N. Gorban, V.I. Bykov, G.S. Yablonskii, Macroscopic Clusters Induced by Diffusion in Catalytic Oxidation Reactions, Chem. Eng. Sci., 1980. V. 35, N. 11. P. 2351-2352. .
157. A.N. Gorban, V.I.Bykov, V.I.Dimitrov. Marcelin-De Donder Kinetics Near Equilibrium, React. Kinet. Catal. Lett., V.12, No.1, P.19-23(1979).
158. A.N. Gorban, Priori evaluation of the region of linearity for kinetic-equations, React Kinet Catal Lett, 10 (2), 149-152, 1979
159. A.N. Gorban, Invariant Sets for Kinetic Equations, React. Kinet. Catal. Lett., 1979, V.10, P.187-190.
160. A.N. Gorban, Sets of Removable Singularities and Continuous Mappings, Siberian Math. Journ., V.19, P.1388-1391(1978).
161. A.N. Gorban, V.B. Melamed, Certain properties of Fredholm analytic sets in Banach-spaces, Siberian Math J, 17 (3), 523-526, 1976.
Selected invited talks 2006-2016
· Keynote talk “The Blessing of Dimensionality: Separation Theorems in the Thermodynamic Limit” 2nd IFAC Workshop on Thermodynamic Foundation of Mathematical Systems Theory (TFMST II), Vigo, Spain, 28-30 September 2016.
· Invited lectures (and the opening of the School) “Derivation of hydrodynamic equations from kinetic theory” at the Imperial College, CDT in Fluid Dynamics across Scales: Summer School 11-15 July 2016.
· Invited plenary lecture “Measure Concentration effect in Machine Learning”, 9th Siberian Congress of Women-Mathematicians May 17 2016.
· Plenary talk “Elusive slow manifolds and hydrodynamic limits without small parameter”, Conference “Hilbert’s Sixth Problem”, University of Leicester, May 02-04, 2016.
· Invited plenary lecture, “Paradoxes of randomized choice of basis”, Neuroinformatics-2016, International Conference on Artificial Neural Networks, Moscow 25-29 April, 2016.
· Keynote lecture “Lyapunov functions and stability of kinetics: .from Boltzmann to present days” at the MaCKiE 2015 “Mathematics in (bio)Chemical Kinetics and Engineering 2015” Conference in Ghent, July 3rd.
· Invited lecture “Evolution of adaptation mechanisms: adaptation “energy”, stress, and oscillating death”, at the conference “Modelling Biological Evolution 2015: Linking Mathematical Theories with Empirical Realities”, University of Leicester, UK, April 28 - May 1, 2015
· Invited Plenary talk “Invariant manifolds and hydrodynamic limit in kinetics” at the Conference “Collective Behavior: Macroscopic versus Kinetic Descriptions,” Imperial College, London, May 2014.
· Invited Lecture: “Detailed balance: background and consequences“, LMS Workshop "Mathematics of chemical reaction networks", Portsmouth, June 2014.
· Invited Lecture “Dynamics of Correlation in Adaptation and Measurement of Stress”, Institut Curie, Paris, 03 April, 2014.
· Keynote talk “Geometry and Topology of Data Spaces” IDEAL 2011, The 12th International Conference on Intelligent Data Engineering and Automated Learning, Norwich, UK.
· Invited plenary lecture “Entropies and uncertainty of uncertainty” International Conference "Modern Problems of Mathematics, Informatics and Bioinformatics", devoted to the 100th anniversary of A.A. Lyapunov, Novosibirsk, Russia, October 11-14 2011.
· Invited talk “Time-step expansion and conditionally stable invariant manifolds in LBM models” Lattice Boltzmann Workshop, Mathematical Institute, University of Oxford, UK, 1 - 2 September 2011,
· Invited talk “Principal graphs and topological grammars for data approximation” Workshop on Manifold Learning, Hausdorff Research Institute for Mathematics HIM, Bonn, Germany, May 2011.
· Invited talk “Entropies”, Workshop on Theoretical Aspects of High-Dimensional Problems and Information-Based Complexity, Hausdorff Research Institute for Mathematics HIM, Bonn, Germany, July 2011.
· Invited talk “Elastic and pluriharmonic graphs as universal approximants” The 3rd International Conference of the ERCIM (European Research Consortium for Informatics and Mathematics) on Computing and Statistics 2010, London, UK, 10-12 December 2010.
· Invited talk “Geometry of data sets” ESOF2010 (Euroscience Open Forum, Torino, July 2-7, 2010.
· Invited plenary speaker “Limiters for LBM”, 19th International Conference on the Discrete Simulation of Fluid Dynamics (DSFD 2010), Roma, 5-10 July 2010.
· Invited Mathematician. Pattern Formation Workshop. IHES, Bures-sur-Yvette, France, January 2010.
· Invited speaker, “LBM stability from the numerical mathematics point of view” Fluid-Kinetic Modelling in Biology, Physics and Engineering, September 2010, Isaac Newton Institute, Cambridge.
· Invited speaker, "Dispersive oscillations, limiters and non-oscillatory LBM" Oxford LB workshop, Mathematical Institute, University of Oxford, September 13-14, 2010.
· Invited talk, “Mathematics of Natural Selection”, Sobolev Mathematical Institute, Novosibirsk, Russia, April 2010.
· Invited talk, “Invariant manifolds for model reduction (with examples from physical and chemical kinetics)” University of Aberystwyth, UK, October 2009.
· Invited talk at the 2nd International Symposium on Neural Networks and Econophysics: from superconducting junctions to financial markets, Loughborough, UK, 13-17 June 2009.
· Invited talk “Dominant Systems for Multiscale Reaction Networks”, MACKIE-2009: International Workshop on Mathematics in Chemical Kinetics and Engineering, Ghent, Belgium, 8-11 February, 2009.
· Keynote talk “A dreaming machine with ghost memory states” A4A6 – Algorithms for Approximation VI Conference, Ambleside, Lake District, UK, 31th of August – 4th of September 2009.
· Invited talk “From simple kinetics to fluid dynamics: exactly solvable reduction problem”, Landau seminar at the Loughborough University physics Feb. 25, 2009;
· Invited talk “Dominant systems and self-simplification in multiscale reaction networks” Warwick Systems Biology seminar, University of Warwick, 20th Jan, 2009.
· Invited talk “University of Leicester: Applied Mathematics for Systems Biology” at the Workshop “Systems biology of signalling in cancer”, Oct. 9-10, 2008, French Embassy, London.
· Invited talk “Branching principal components and topological grammars for data analysis and dimension reduction” Complexity Colloquium, University of Bath, Dept of Mathematical Sciences, 18th February 2008.
· Invited talk “Dynamics of large systems with inheritance (selection theorems and finite-dimensional asymptotics of some infinite-dimensional systems)” Maths Colloquium at the University of Kent, 25th February 2008.
· Invited talk “Invariant manifolds for model reduction”, Applied Mathematics seminar at the University College London, 03 March, 2008.
· Invited talk “Invariance Equation”, Oberwolfach Workshop “Material Theories” ID 0751, Oberwolfach, Germany, December 16th - December 22nd, 2007.
· Invited talk “Dominant systems for asymptotic analysis of reaction networks”, Centre for Mathematical Biology, Oxford University, 29th February 2008.
· Invited talk “Limiters in lattice Boltzmann methods”, Center for Scientific Computation and Mathematical Modeling, University of Maryland, MD, USA April 9, 2008.
· Invited keynote talk “Self-simplification, dominant systems and 0-1 laws in multiscale reaction networks” Workshop of the London Dynamical Systems Group, at UCL on the theme of "Nonlinear dynamics of chemical and biochemical reaction networks", 28 May 2008.
· Invited talk “Branching principal components and topological grammars for data analysis and dimension reduction”, Rutgers University (Camden), Department of Math, NJ, USA, March 28, 2008.
· Invited talk “Invariant manifolds for model reduction in physical and chemical kinetics” Department of Mathematics, University of Durham May 5th, 2008;
· Invited talk “Mathematical minimalism in analysis of genetic taxts”, Workshop “Think Tank on Statistical Semantics of Genomes: From Sequence to Function”. Epigenomics Project, Genopole, Evry, France, 27-29 May 2008.
· Invited lecture “Model Simplification and Self-Simplification in Chemical Kinetics” at the International Conference on Modeling in Chemical and Biological Engineering Sciences, Bangkok, Thailand, 25-27 October 2006.
· Visiting scholar and invited talk “Dominant systems for reaction networks” at the Courant Mathematics Institute, NY, April, 2007.
· Invited lecture “Informational disassembling of biological machines” At the International Workshop “Theoretical Approaches for the Genome,” Annecy, France, November, 2006.
· Invited talk “Invariant manifolds and the thermodynamic projector for model reduction in chemical kinetics”, 11th International Conference on Numerical Combustion, Granada, Spain, April 23-26, 2006.
Some other recent talks
· The five factor model of personality and evaluation of drug consumption risk, 2015 Conference of the International Federation of Classification Societies, University of Bologna, Italy, July 6-8, 2015.
· Bootstrap test of ordered RIG for multiple testing in genomics of Quantitative Trait Loci in yeasts, 2015 Conference of the International Federation of Classification Societies, University of Bologna, Italy, Italy, July 6-8, 2015.
· Further Results on Lyapunov-Like Conditions of Forward Invariance and Boundedness for a Class of Unstable Systems, 53rd IEEE Conference on Decision and Control, Los Angeles, California, USA, 15-17 December 2014 (Joint work with I. Tyukin)
· Computational diagnosis of canine lymphoma, 2nd International Conference on Mathematical Modeling in Physical Sciences 2013, Prague, September 2013 (Joint work with E M Mirkes, I Alexandrakis, K Slater, R Tuli)
· Multiscale principal component analysis, 2nd International Conference on Mathematical Modeling in Physical Sciences 2013, Prague, September 2013 (Joint work with A A Akinduko)
· Is it possible to predict long-term success with k-NN? Case study of four market indices (FTSE100, DAX, HANGSENG, NASDAQ), 2nd International Conference on Mathematical Modeling in Physical Sciences 2013, Prague, September 2013 (Joint work with Y Shi, T Y Yang)
· Scene Analysis Assisting for AWB Using Binary Decision Trees and Average Image Metrics., IEEE Conference on Consumer Electronics, 10-13 January 2014, Las-Vegas, USA (Joint work with K.I. Sofeikov, I. Romanenko, I. Tyukin)
· Explicit Reduced-Order Integral Formulations of State and Parameter Estimation Problems for a Class of Nonlinear Systems, 52-th IEEE International Conference on Decision and Control (10-13 December, 2013, Florence, Italy), (Joint work with I. Tyukin)